Category: Conventional Wisdom

Will 2020 See The Extinction Of The Red-eyed Monks?

For those of you not familiar with what has been called “the hardest logic puzzle in the world”A, The Blue-eyed Monk problem or Blue-eyed Islander problem (Version 2), check out the above reference links. For what it’s worth, that “hardest” title is probably an exaggeration. But my new version, inspired by recent events, might be harder.

In this version of the famous logic problem, there are a number of monks on this remote island. All of them are “perfect logicians”. Every monk sees every other monk every day, but they are rugged individualists who never talk to each other or communicate in any way. They also take full responsibility for their actions and obey all rules and protocols. (Yes, this problem is entirely fictional.) Strangely, there are no mirrors or reflective surfaces on the island. The ferry visits the island every night to drop off supplies. It would take the monks to the mainland, if necessary. But none of the islanders wants to leave and no strangers are allowed on the island. In this version of the problem, all of the monks have red eyes.

One day, almost all of the monks noticed that one of their peers had blue eyes, but they all continue to go about their lives. Many days later, it is noticed (by almost all of them) that two of the monks now have blue eyes. Still, life goes on. This trend continues with a slowly increasing frequency until many, many days later, the first monk to have developed blue eyes is found dead. Doctors on the mainland soon discover that some as-yet-unknown, but contagious pathogen hit the island. The number of monks infected has been growing 2% every day for quite some time. The only visible symptom is the changing of eye color from red to blue. The disease is not contagious until the eyes go blue but then remains contagious until the infected person dies. How it spreads is still unknown, but obviously, direct contact or even close proximity is not required.

By the time the doctors figure all of this out, red-eyed monks have started changing eye color at the rate of one every other day and the second blue-eyed monk has just died. If a blue-eyed monk gets to the mainland in time, they can be cured. but the ferry does have a limited capacity. The monks are pacifists, so there will be no shooting of blue-eyed monks (yes, I might have a personal stake in this directive). All of this information was left on a large sign at the ferry dock the next day.

So what do the monks do? Will they go extinct? Will 2020 see the end of all logical thought on this planet? Only you can answer that question. Good luck! Leave your answers in the comment section below.

To see the Note click here.To hide the Note click here.
In the interest of full disclosure and transparency, I have addressed this problem before. After much fumbling, I did come up with a better (faster) solution, which was widely regarded as cheating (see comment to “The Blue-spotted Monks Revisited”.

A Pair Of Perspectives On Pearls

Several Sundays ago, our pastor began his sermon by talking about the world’s largest pearl.

To see the Note click here.To hide the Note click here.
This pearl, which was just recently revealed after being hidden for ten years, is 26 inches long and 12″ wide, weighing 75 pounds. That’s over 2½ times longer and five times heavier than the previous record-holder, which was found in another giant clam near the same Philippine island in 1934 (both the diver and the clam lost their lives in the earlier case).

Filipino Fisherman Reveals 75-Pound Pearl He Kept Hidden For A Decade.

Our preacher used the pearl as an example of how God can take an irritant and help you turn it into a treasure. I believe that is a common way of looking at this from a human perspective. But for some reason, I saw the issue differently.

Another Possible Moral To This Story

Turning trash into treasure – is that what the clam was actually trying to do? Does the clam even know that the old irritant now has such great value (estimated to be over a hundred million dollars)? Was this 75-pound object, which had been growing for over a hundred yearsA, actually less irritating to the clam than the original grain of sand? I suspect not!

The preacher could have used this as an allegory, showing how man, because of pride, will try to solve a problem by himself but fail, despite putting a great deal of effort and time into it. And, as is often the case, he could even make the situation worse, not better. “But look how pretty I made it.” Can’t you just see that giant clam trying to sing Frank Sinatra’s “My Way”lyrics, video (but failing, of course, because it has a 75-pound lump of calcium in its mouth)?

Is There A Third Possibility?

One of the beauties of life is that some situations can share many lessons. Reality is like that. Even as I was writing this, a third perspective began taking shape in my mind. Of course, I ignored it. But if you found another pearl of wisdom in this parable, please share in the comment section below. Thank you, and thanks for listening.

Not Quite Clear On The Concept “Innocent Until Proven Guilty”

Listening to discussions on Facebook about the Brett Kavanaugh nomination, I was surprised and disappointed to see the “innocent until proven guilty” principle so often misapplied (and in two different ways).  It became clear to me that a lot of people just don’t understand the concept.

A Larger Doctrine

When something is being awarded to somebody, whether it is good, bad, large, or small, most people would like to think the recipient deserved the award.  It is the presenter’s responsibility to make sure that’s the case.  The more extreme the action, whether reward or punishment, the more effort the presenters should take to see that the award has been earned.

The Bad

When the award is a punishment, this doctrine takes the form of “innocent until proven guilty”.  If the death penalty is under consideration, for example, we need to go to great lengths to be sure we aren’t making a mistake.  I’ll save the discussion of the two types of possible errors – letting a murderer go free vs. hanging an innocent person – for another day.

The Good

When the action under consideration is a reward, one would expect some law of symmetry to apply, and it does.  In this case, the slogan “innocent until proven guilty” has no place.  Whether it is the Mega Millions jackpot or the Nobel Prize, one does not assume a prospect is ‘innocent’, or deserving, until proven otherwise.  It is up to the claimant to prove they deserve the award.  For the Mega Millions jackpot, that would be by showing the winning ticket and some form of identification.  The Nobel Prize has even more stringent requirements.  Republicans have no trouble applying this principle to welfare recipients but seem to get tripped up when it comes to Presidents and Supreme Court nominees.

The Ugly

In either of the above cases, it is well understood, as stated above, that the candidate will be fully vetted.  And the more significant the award, the more serious the investigation.  For someone to insist that a candidate is “innocent until proven guilty”, especially for a reward, and then refuse to hold a meaningful investigation into any evidence of guilt is the height of duplicity.  But that seems to be the current state of the Republican Party.  It hasn’t always been this way.

Anyone with a logical alternate interpretation of the facts is welcome to share.  You can be sure the civility of this discussion will be maintained.

Please Help! The Special Theory Of Relativity Is Haunting (or is it Taunting) Me!

A long time ago (when I was in the sixth or seventh grade) in a galaxy far, far away (namely Southern California), I was introduced to Einstein’s Special Theory of Relativity by way of a story about two astronauts on different spacecraft watching a bouncing-light-beam clock, and I was really impressed. But upon further review as I was chewing my cud (See definitions of “ruminate”), as I was wont to do walking home from school, it didn’t seem to make as much sense. I developed some questions but didn’t know where to get answers, and as life pressed on my attention wandered elsewhere, and everyone lived happily ever after. . .

Until recently. In the last year, the subject has come up several times, the questions seem to be the same, and I still don’t know where to turn.

The Story

Although not exactly as I remember it, www.dummies.com1 describes a similar thought experiment in the second section, “UNIFYING SPACE AND TIME”, with a spacecraft traveling at ½ the speed of light, but doesn’t give much explanation. A more detailed explanation can be found in The Star Garden2.

The Problem

“Time Dilation”, Section 7.2.2 of Reference 2 concludes

“The time between heartbeats is also slower, and so from the perspective of a stationary person, a moving person appears to be living their life at a slower rate. Conversely, from the perspective of the moving person, the stationary person seems to live their life as if it is being fast-forwarded. If they travel fast enough, then they could see the stationary person age before their eyes.”

My problem with that conclusion is that based on the second paragraph of Section 7.1 at the beginning the article, which states

“there’s no such thing as absolute speed or velocity, and something can only be said to be moving at a constant velocity relative to something else. In the same way, something can only be said to be stationary relative to something else”,

how do we really know which astronaut is supposed to be aging before our eyes? What if we put a bouncing-light clock on each spacecraft? Would it explode?

The authors of Reference 2 seem to address this issue at the bottom of the next section, 7.2.3, where they say

“The twin paradox

The twin paradox asks why the astronaut can consider themselves to be moving and the Earth to be stationary, when Galileo’s relativity shows that there’s no such thing as absolute velocity. Why can’t the astronaut consider themselves to be stationary while the Earth moves away at tremendous speeds?

The answer is acceleration. Galileo’s relativity applies to inertial – that is non-accelerating – reference frames. The fact that the astronaut must have accelerated before getting to such high speed means that they know they are the one that is moving.”

To me, this sounds bogus; any acceleration before or after the experiment should be immaterial. Let’s have three observers; one person remains on Earth while two astronauts board different spacecraft, each leaving the Earth in opposite directions and reaching similar stable speeds well in excess of ½ the speed of light (meaning their relative speed would exceed the speed of light in a non-relativistic world). Each of the observers has their own bouncing-light clock. If you start counting after their speed stabilizes, exactly how do each of the three observers see the ages change for the other two?

One Last Question

A question that one might ask in each of these scenarios is “how does the state of the bouncing light in one spacecraft become known to the other observers?” Reference 1 states that Amber, on a different spacecraft, would see the bouncing light travel further between bounces, as if Amber had super X-ray vision and/or was otherwise experiencing the light beam in real time. How does that work? If she had to wait for reflected light rays from the event to reach her eyes, would that affect the apparent outcome in any way?

One phenomenon that may or may not have anything to do with the solution to this problem involves ocean waves. In deep water, a wave’s speed is nearly proportional to the square root of its wavelengthA,

To see the Note click here.To hide the Note click here.

S \cong 1.251 \sqrt{W}

where S is the wave’s speed (measured in meters per second) and W is its wavelength (in meters).
For shallow water waves, the speed is proportional to the square root of the depth.

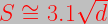
S \cong 3.1 \sqrt{d}

where d is the water’s depth (in meters).


but in all cases, it is much less than the speed of light. If an observer were to watch the crest of a wave as it moved along a seawall, or along any imaginary line that wasn’t along the wave’s direction of travel (directly away from a point source, or in the direction of the wind, or perpendicular to the wavefront, etc.), then the apparent speed would be greater than the calculated or expected speed, and as the angle of that reference line approached 90° to the direction of travel, the apparent speed would approach infinity.

To see the Note click here.To hide the Note click here.

A = \frac{S}{\cos \theta}

where A is the apparent speed, S is the expected speed, and θ is the angle between the reference line and the direction of travel.


which is well above the speed of light. As far as I know, this has no implications or gives no reason for hope for wannabe time travelers.

In Summary

So now you see my dilemma. To repeat the title plea, please help me understand. A crucial early step in solving any problem may be asking the right questions. Finding those should be as important, and in some cases may be as difficult as answering them. So let’s get started. Thank you for your help. If I do figure it out without your help, I’ll let you know.

We Can Simplify Our Student Grading System

In the works, I have two different questions for you:

  1. ‘Do Medium-sized Egos Really Exist?’, and
  2. ‘Should Law Enforcement Officers Be Allowed To Use The “I was afraid for my life” Defense?’

Both of these require some preparation/research, but I hope to have them ready before too long.   For now, I’ve chosen a lighter topic about a scheme that, because it’s not being implemented as designed, could well be simplified.

Some Background

When I started school, we got one grade, from A to F (I never learned why E was left out), to represent our mastery of the subject.   Then, at some point, they introduced a separate grade for effort (from 1 to 3) and another for conduct (also A through F, also without the E). These were promoted as independent variables that could give more insight into the performance of one’s child.   I soon had reason to question the independence of these variables.

What’s The Best Grade You Can Get

Conventional wisdom tells us that the highest grade one can get would now be an A1A.   I’m not here to discuss the merits of bad behavior, so we will focus only on the first two symbols.   To me, it was obvious that an A3 would be more desirable.   Here’s why –

Suppose it’s a leap year and you are betting on track events at the Summer Olympics.   In the first heat, the first place runner comes in with a time of, say, 4:00.00. At the end she is visibly spent (lying on the ground, breathing heavily, and sweating profusely).   Her grade would clearly be an A1.   In the next heat, the winner has the exact same time but isn’t even breathing hard.   I would give her an A3. Keep in mind that it is not uncommon for runners in the early heats of big events to pace themselves to save some effort for later heats, if they can afford to.  

Of course, both runners advance to the finals with the best times.   Again, conventional wisdom gives the higher grade to the first runner. But tell the truth – which one are you betting your hard-earned money on in the finals?

My Experience

So you can see what grade I was trying for.   But the truth is teachers don’t give A3 grades, even if you never turn in your homework.   This isn’t a case of political correctness (whereby we fashion our remarks based on the possible objections of imaginary people with hyper thin skins or real fools priding themselves on how easily offended they can be). It is another common problem in the political arena whereby people refuse to let facts get in the way of their idea of the way things should work in their perfect (but grossly oversimplified) world.   In their view, the very fact that you got an A proves that you were trying really hard because hard honest work is what made America great.  

The problem is that once you link those previously independent variables (effort and results), you are really only working in a one-dimensional world. You don’t need two grades to adequately describe it.

Looking From The Other Side

But you may be saying to yourself “Silent, you are the anomaly!   Only the very rare person who can find a task at which they can succeed without unbelievable effort would have the luxury of taking your position on this topic”.   If you really think failure is the norm, then answer this:  

Do you really think someone who, for whatever reason, didn’t meet the minimum requirements for success in this class, would prefer an F1 over an F3?   From what I’ve observed, the opposite has usually been the case.   If you give him an F1 you are saying “bless his little heart, he gave it his best shot but is just too stupid to make the grade”.   That may even be true, but giving him an F3 gives him an alibi (or more accurately, reinforces the excuses he’s been giving even without your blessing) that he’s really very, very intelligent, but just didn’t put forth the effort.

I’m not saying to give all failures a “3” – you could just make the variable independent, open your eyes, and give the student whatever they truly earned.

Conclusion

There are actually two ways to cure this problem: we could start treating effort and results as the independent variable they are (which is probably too agonizing a task for most teachers). Or we could just stop giving the effort grade.   I propose the latter.   What do you think?

When Sailors Should Split Tacks

American inventor Thomas Edison once said “Genius is one percent inspiration, ninety-nine percent perspiration”A. From my experience, when you are competing, whether for business or pleasure, or trying to solve a problem, or just trying to get something done, you can usually do pretty well without that stroke of genius if during the remaining 99% of the time you can just keep from screwing up.

A Sailing Example

One summer I had the opportunity to race sailboats by donating the perspiration needed to handle the sails.   Since sailboats can’t sail directly into the wind, which is often exactly where you need to go, you must regularly choose which side of the wind is best, or which side of the course is best, or . . . the bottom line is that in sailboat racing, as in life, there are plenty of decision-making opportunities.  

If we happened to get behind early in the race, by the time we got to a point that needed a decision, our competition had already gotten to that point and had already made their decision.   Our skipper, reasoning that we would never catch up if we did everything our competition had done, invariably would make the opposite choice at that point (hence, splitting tacks, or sailing on the opposite side of the wind as our competition).   More often than not we would get further behind.   As it turned out, we didn’t win many races that summer. Now I will use just a little math to show you why not.

The Math

Without divine intervention or that long-awaited flash of inspiration, after a short time the leaders in this race will be the ones that make more correct moment-by-moment decisions. When our skipper got to his decision point, it is reasonable to assume that the competition ahead of him is batting above 500D and already chose the short path. If the current leader has a success rate of, say 70%, then by blindly taking the other path, our skipper was limiting his success rate to 30%. This is NOT a winning strategy.

The more prudent leader would have chosen his battles; he would have evaluated every decision independently – more often than not this means he would have made the same choice as his competitor (assuming his own success rate is high enough to be competitive – certainly higher than 50%) – and he would bide his time while waiting for the competition to make their mistake. When his own evaluation led him to a different decision, he would quickly recheck his work (out of respect for his competitor’s 70% success rate) and then he would pounce.

A Non-sailing Example – Rush Hour Traffic

“Rush Hour”, referring to those busy couple of hours in the morning and another couple of hours in the afternoon when everybody is commuting to or from work at the same time and traffic is congested (as opposed to that time of day when Rush Limbaugh is delivering his political commentary), implies an urban environment, which implies a larger grid of streets and thus a richness of decision-making opportunities not completely unlike a fleet of sailboats tacking upwind, but familiar to a much larger segment of the population.  

Many of you may have carpooled with somebody with the mentality of the skipper described above: either there is some sort of accident or s/he misjudged traffic again and finds him/herself behind schedule and facing the growing possibility that they will be late for work.   Lacking patience or maturity, they assume the traffic must be better on one of the many alternative routes and blindly makes a turn (tacks) at the next intersection.   When they discover that this path is also blocked, they immediately move to Plan C, then D, and so forth.   Each maneuver has a small cost, which rapidly adds up, and then the path actually starts to get longer and they continue to dig themselves a deeper and deeper hole (oops, that’s not a sailing reference).   The math is similar to that above.  

To mix metaphors even more, compare this to the hitter swinging too hard for a home run.   The problem is that in this game, after each errant swing the outfield fence is moved ten yards further away.   Although still mathematically possible (at first), the odds of that game-winning home run drop with every swing.   Those are the perils of panicking, shutting off your brain, closing your eyes, and trying to slug your way out of your problems.

The Moral

As you might have guessed, this article is not really about sailing, or traffic, or baseball. Blindly splitting tacks is a tactic of desperation.   Desperation is often a result of one’s fears getting the best of them and may be one of the consequences of ignorance.   It is never expedient to shut off your brain to save time (by the same token, except for specially trained pilots in specially designed aircraft, no self-respecting pilot would willingly turn off an airplane’s engines while still in the air), yet people try it every day.   This is what happens when you panic.   So get a grip!   Just as in the sailing example, the prudent driver would carefully evaluate every decision (the more you practice, the easier it gets) instead of assuming the worst, bide your time, and make your bold move only when the conditions are right.

Simple English: The Problem With The “If” Statement

You are probably very proud of your grasp of English (unless you live in South Florida, in which case you may not give a damn).  And yet I have seen plenty of people whose lack of understanding about basic structures like the “If” statement

To see the Note click here.To hide the Note click here.
The next article in this series will discuss how misunderstandings about the conjunction “or” have caused so much trouble.
cause them to make terrible assumptions.

An Example

Suppose a young child is misbehaving to the point that the caregiving parent decrees “If you don’t knock that off, I’m going to paddle you” (This is an old example; I’m sure nobody would ever actually do that today 😉 ). As young children have been known to do, for whatever reason, the child continues with its behavior. The parent repeats the statement, with added emphasis. Nothing changes. The parent soon throws their hands up and says “wait until (your other parent) gets home”.

The parent’s first decree, like all “if” statements, had two parts; a condition and a consequence (joined by the conjunction “if”), with the understanding that if the condition is true, then the consequence will occur. It’s simple enough that even a young child can understand it. If the condition is met and the consequence is not accomplished, then the statement would be considered false. In short, the child knew that the parent was lying.

Now suppose the non-caregiving parent comes home, sees the objectionable behavior, makes a similar decree, and then the first parent points out that they had already made that decree to no avail. The child, for whatever reason, stops the objectionable behavior. To everybody’s surprise, the second parent paddles the child. Although the child and many of you listeners may think bad thoughts about this parent, one thing you can’t call him/her is a liar.

The Problem

As you can see here, the problem with the “if” statement is that is incomplete in the sense that it only addresses what happens when the condition is true, remaining completely silent to the possibility that the condition could be false.  This allows most people to make the assumption that if the condition is false, the opposite of the consequence must occur.  As the young child in our example learned, that assumption would be a mistake.

The Solution

Don’t make stupid assumptions.  As your lawyer would tell you, get it in writing.  In the above example, since the second parent didn’t make any promises about what would happen if the behavior did stop, s/he can’t be accused of lying.  If this example bothers you, I’m sure the second parent told the child afterward that the paddling was for not obeying the first parent, in which case we would be unable to judge the truthfulness of their claim until after the right set of conditions are met following some later episode of misbehavior (guesstimating any change in likelihood of that future misbehavior based on recent events  will be left as an exercise for the reader).  To lawyers, mathematicians, and the like, the parent’s explanation doesn’t matter to this case and is unnecessary.

P.S.

Logicians have named operators (or functions) fulfilling all sixteen patterns of truthfulness or falsehood of expressions based on the truthfulness or falsity of two variables, such as the condition and consequence of the “if” statement described above.  Engineers call the statement that yields the results you thought the “if” statement provided the “exclusive nor” function, “nor” being short for not or, meaning “giving the opposite results than the ‘or’ function”.  Some refer to it as logical equality.  In English, it would be represented by a sentence including the phrase “If, and only if”, such as “I will ground you for the rest of your life if, and only if, you do not stop screaming this very second”.  If that type of statement had been the norm in this household, the non-caregiving parent, upon hearing the lack of results achieved by the other parent, was still free to add other (most likely “or”) clauses (to be discussed in a later article) to his/her decree.   If you are now totally confused, please do not sign any document containing more than six words before consulting an attorney, or at least a mathematician.  On second thought, in cases like this, I would stick with the lawyer.

The Blue-spotted Monks Revisited

If you are not aware of the Blue-spotted Monk problem, or haven’t seen my previous post (in which I made an error in logic), please visit The Problem Of Blue-spotted Monks.

Did you ever wonder what would happen if, as a cruel joke, it had been reported to the monks that one of them had the dreaded blue spot disease when in fact nobody was afflicted? (Am I really the only one here with a slight sinister streak?) Since none of the monks saw a spot elsewhere, they would each assume it was them that was infected and the very first day all the monks would have started to gather at the exit station. One of them, as he approached, would notice that none of the others had a blue dot and would start to chuckle to himself, thinking “these clowns can’t even count”. The others, hearing him laugh, would look around for the first time (until then they were so sure of their logical talents that they hadn’t even bothered to check), and by the time he stopped laughing the rest would have disappeared into the forest. Then it would occur to him that maybe he didn’t have a spot either. When word got back to the Guru, the laugher would be expelled for violating the “no communication” rule, but it wouldn’t affect the solution because the other monks only counted the peers that had spots on their forehead and he was never missed.

Plan B (I named this scheme in honor of B, who first put things in perspective for me. If this plan turns out to be flawed, like the last, I take full responsibility.)

When answering nature’s call in the middle of the night a few days after accepting B’s explanation about why the monks had to start at zero, it struck me that since a monk was really only concerned with three possibilities in the number of blue spots anybody has seen, modulo arithmetic might give a way to synchronize everybody’s universe or get everybody on the same page, so to speak. Plan B calls for everyone to start counting not at zero, but at the last multiple of six. For example, the person who saw ten blue dots knows that there are either:

  1. ten afflicted, not including himself, which means there are ten people who see only nine spots.  Everybody else sees ten.
  2. On the other hand, if he is blue-spotted, there are ten others like him who see ten spots and everyone else sees eleven.

Those who see nine spots know that those who see eleven don’t really exist, and those that see eleven know that the nine-seeers don’t exist. The monk that sees ten must consider each of the other two cases, but not both at once.

Under Plan B he would start counting at six, as would the possible people who saw nine, and those potential people who saw eleven. If everyone knew to start at six, the nonexistent people who saw only six spots would be gone before the second day (we’ll discuss them again shortly), and since that won’t happen, the nonexistent people seeing seven spots will leave on Day 2, etc. Our guy knows he can sleep in until Day 4, when the really possible nine-spot sighters would be scheduled to leave. If he saw spots on Day 5, he would turn himself in and everybody else would live happily ever after.

Starting the inductive thinking process, the first six possibilities start counting at zero, just like the old days. We’ll call that their landmark. As the logic countdown continues past the next landmark (which would be six in this scheme), the hard thing for me was knowing who would start using it first, or even if it was possible to make the switch if that person needed to wait for the person ahead of him (who is still using the old landmark) to make his move. I had the hardest time reconciling the notion that you needed to wait for the people ahead of you with the notion that those people don’t exist.  It turns out the solution was easier than I imagined.

In Plan B, if the number of spots you see happens to be six (or any exact multiple thereof), your dilemma is that the possible person who sees five spots started counting at zero, and won’t budge until Day 6. The guy who sees seven spots will start counting at six, and is depending on you to leave now (Day 1) or else he’s lost. Go to the exit point on Day 1. If you are not infected, there will be a very large crowd heading for the exit with no spots on their head while six people with a spot sit comfortably at home. When you spot your peers, you will avoid the crowd and head home knowing that those six afflicted people will all leave on Day 6 as scheduled, and all is right with the world. If you do have the spot, there will be six others with spots heading out that day with you while everyone else waits patiently at home. When those who originally saw seven spots wake the next morning, you will be gone and the problem will be solved.

What Next?

Lately this problem has turned into an on-again-off-again obsession for me. I first saw a different version of the problem when I was much, much younger; I didn’t figure it out for myself but the answer made perfect sense. Just a few weeks ago, I ran across the spotted monk version I discussed in my last post and again, when reading the answer, I was completely satisfied (although I felt for the commenters who couldn’t accept that it would take 100 days for 100 blue-spotted monks to turn themselves in). Days later, while on a walk contemplating even more difficult (but unrelated) relationship issues, an answer just came to me out of the blue, which is the answer I last posted. It was flawed, and when B. gave his “parallel universe” explanation for why we needed to start at zero, I thought it made even more sense than the conventional answer did, and I was again happy.  Several days after that, the modular arithmetic idea just came to me (as discussed). Then it was only my day job and other commitments that slowed me from working toward this solution. But we are not actually finished yet.

Calling All Logicians

All I’ve done so far (if I got it right this time) is to show that starting at zero is not strictly necessary.  Plan B is not the only possible plan, however.  In fact, I doubt it is the best or fastest plan (I suspect that using a smaller modulus might be helpful).  For the monks to abandon zero as their global landmark there would have to be an understanding that there was a single, logically optimal plan to replace it.  Based on my difficulties wrapping my mind around the issues so far, I don’t feel I qualify for the “perfect logicians” requirementA of this monastery.  It’s just as well; as an aging curmudgeon, that vow of silence probably wouldn’t have worked for me for very much longer anyway.  I’m hoping that the real experts will take it from here and God will finally allow me to let go of this problem.  If you do see a flaw in this scheme (a check of the references will show it would not be my first mistake on this problem), let me know. I may not be able to fix it, but in keeping with journalistic standards, I am willing to admit and advertise the error. Thank you.

Flawed Logic: The Problem Of Blue-spotted Monks

I recently ran across the Problem of the Blue-spotted Monks again at https://richardwiseman.wordpress.com/2011/04/04/answer-to-the-friday-puzzle-98/.  Actually, this is a slight variation of the well-known Blue-Eyed Monk problem that can be found at https://en.wikipedia.org/wiki/Common_knowledge_%28logic%29, among other places. One site even called this problem “The Hardest Logic Puzzle in the World”A, but that was probably just a case of self-promotion. For today’s discussion, I chose the first version of the problem because it is simpler (we don’t have to worry about the case in which one person has red eyes). If you haven’t done so, go ahead and read the problem. We will discuss the solution in the next section.

Start With Induction

The classic answer uses mathematical inductionD to first consider the (trivial) case in which only one monk has the disease. Then they move on to the case of two monks. Their error begins in the case of three infected monks, assuming that the monks were required to start back at one in making their individual analysis.  That is wrong; in the comments section of some of the references, several people take issue with this assumption.  I believe this to be a misapplication of the induction process.  The monks have only to consider two possibilities; either they are infected or they are not. For the sake of argument, let’s say there are ten infected monks. Most of the monks will see ten fellow monks with blue spots. Ten of the monks will see nine monks with blue spots. None of the monks will see only one monk with blue spots, or just two monks with blue spots, etcetera. Those monks seeing ten spotted monks have only two possibilities – either there are ten infected monks or there are eleven. Those monks seeing nine spots need only consider the possibility that there are either nine or ten monks infected. Most of the monks, in considering their first possibility (that there are only ten infections) realize that those ten, in considering the possibility that there are only nine infections, must allow for the possibility that there are nine monks who see only eight infected monks. With the information available, nobody sees any reason to consider any other lesser possibility. Just like in the conventional solution, each monk, having two possibilities, must allow the lesser possibility (which means they are not infected) to resolve itself first before concluding that they are infected and turn themselves in. All of the monks know that the least number of infections that any of them must consider is eight, not one. The first day nothing would happen. The second day, the monks that saw only nine other spotted monks will conclude that the possibility of anyone sighting eight spotted monks was groundless, so they will all turn themselves in. The third day, those who saw ten spotted monks will all breathe a sigh of relief.

Considering The Second Possibility

Now we need to look at the big picture.  This isn’t rocket science.  Why hasn’t anybody seen the error in conventional wisdom before today?  I, like the monks, must consider the possibility that I am the one infected.  If nobody else comes forward with a confirmation of the correct answer soon, I guess I’ll be forced to turn myself in.  Please hurry.

A Better Way To Handle The Harambe Incident

For those who haven’t heard about the gorilla named Harambe that was shot ten minutes after a toddler fell into his enclosure at the Cincinnati Zoo around 4 pm on Saturday, May 28, 2016, here is as good a source as any: Gorilla killed after 4-year-old falls into zoo enclosure. Apparently, authorities had both a tranquilizer gun and a rifle at their disposal, and chose the rifle to fatally shoot the gorilla even though the boy hadn’t yet been seriously injured because they were afraid that the tranquilizer wouldn’t act fast enough. They didn’t have to make that call. Here’s a better way.

  1. Take both the tranquilizer and the rifle. The same person should not operate both.
  2. Have other staff members make themselves immediately ready to rescue the child.
  3. When both weapons are ready, shoot the gorilla with the tranquilizer.
  4. Have the person with the rifle continuously evaluate the threat posed by the gorilla.  If bodily harm from the gorilla is not immediately forthcoming, do not shoot.
  5. If the parents get hysterical while you are evaluating the situation and behave in such a way as to adversely affect the behavior of the gorilla or the judgement of the zoo staff, shoot the parents.  (So as not to make the same mistake as the Cincinnati Zoo staff did Saturday, I guess I should mention that you could use the tranquilizer gun for this if you had the forethought to bring the correct dose – even though at this point it wouldn’t be my weapon of choice.  If you don’t have the correct dose, just pray that the staff isn’t acting under the same level of panic or incompetence as they exhibited with Harambe.)
  6. Rescue the child as soon as practicable.

Although (admittedly based on limited information) I did not think the boy was in danger, and not all witnesses in Cincinnati felt the dangerA, those opinions don’t matter to the success of this plan. Since using the tranquilizer doesn’t prevent the use of the rifle, this plan could not have turned out worse for the child than the plan executed, and most likely would have turned out much better for all concerned. The zoo simply threw away options prematurely based solely on their worse fears instead of facts – that sounds like panic to me, and it sounds very unprofessional.  If you feel differently, feel free to comment.  If you see a reason that this plan would not work, feel free to comment.